侯文莉

安科瑞電氣股份有限公司 上海嘉定 201801

摘要：微型電機(jī)具有體積小、重量輕、便于控制等優(yōu)點(diǎn)，已廣泛應(yīng)用于生產(chǎn)消費(fèi)等領(lǐng)域.為保證微型電機(jī)的性能滿足使用要求，實(shí)時監(jiān)測是的環(huán)節(jié).在傳統(tǒng)的電機(jī)保護(hù)中，信號處理采用的都是模擬濾波器.與模擬濾波器相比，數(shù)字濾波器具有更高的靈活性和穩(wěn)定性。本文提出一種基于FFT算法的電壓信號處理方式，利用FFT可以由輸入序列直接計(jì)算出輸入信號的直流分量以及各次諧波的幅值和相位的特點(diǎn)，大大簡化了諧波分量的計(jì)算。

關(guān)鍵詞：FFT；電機(jī)保護(hù)；數(shù)字信號處理

0引言

FFT是一種DFT的高效算法，基本上可分為時間抽取法和頻率抽取法，把長序列分為短序列，可在時域或頻域進(jìn)行。常用的時域抽取方法是按奇偶將長序列不斷變?yōu)槎绦蛄?，輸出序列為順序序列，而一般的時間抽取法和頻率抽取法處理的長度只有N=2^M。本文主要研究FFT算法在電力監(jiān)控產(chǎn)品中的應(yīng)用效果，不僅能夠有效去除諧波干擾，還可以有選擇地單獨(dú)計(jì)算諧波分量，充分利用了FFT的原位性.

1傅里葉算法的原理

快速傅里葉變換(FFT)是離散傅里葉變換(DFT)的一種快速算法，從物理意義上來看，DFT將時域的數(shù)字信號變換成頻域的離散信號，根據(jù)變換之后的結(jié)果可知時域數(shù)字信號在不同頻率上的幅值，確定時域信號主要分布在哪些頻段上；從數(shù)學(xué)角度來看，ar是將數(shù)字信號變換到幾個正交的坐標(biāo)系中。圖1為時域數(shù)據(jù)的DFT變換。

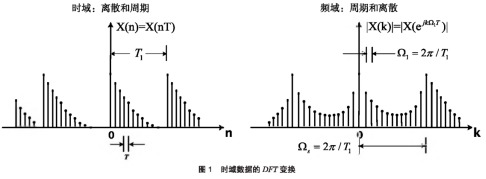
DFT是連續(xù)傅里葉變換的離散形式。模擬信號x(t)的連續(xù)傅里葉變換可表示為：

x(t)經(jīng)抽樣后變?yōu)閤(nT),:T為抽樣周期。設(shè)x(n)為N點(diǎn)有限長序列，其DFT為:

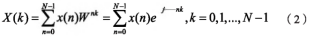
由式(2)可以看出計(jì)算所有x(k)大約需要N²次乘法和N(N-1)次加法，運(yùn)算過程非常復(fù)雜。

一般來說，由于x(n)和W_N^nk都是復(fù)數(shù),X(k)也是復(fù)數(shù)，那么復(fù)數(shù)運(yùn)算實(shí)際上可以通過實(shí)數(shù)運(yùn)算來完成，式(2)則可以寫成：

仔細(xì)觀察DFT的運(yùn)算，利用系數(shù)W_Nⁿ的以下固有特性，可以減小DFT的運(yùn)算量。

W_Nⁿ的對稱性為：

W_Nⁿ的周期性為：

由此可以得到：

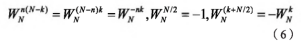
利用這些特性，DFT運(yùn)算中的有些項(xiàng)就可以合并。由于DFT的運(yùn)算量與N²成正比，所以N越小計(jì)算量越小。

2 FFT算法的應(yīng)用

離散傅里葉變換(DFT)和快速傅里葉變換(FFT)是同種變換。FFT只不過是利用DFT系數(shù)W_Nⁿ的對稱性和周期性，可以將長序列的DFT分解為短序列的DFT,然后再按一定的規(guī)則進(jìn)行合并，從而得到整個DFT。本文根據(jù)電機(jī)工作時產(chǎn)生的電壓、電流波形的差異來區(qū)分正常電機(jī)和故障電機(jī)。要找出這種差異，首先需要獲取正常電機(jī)和不良電機(jī)的電流、電壓信號數(shù)據(jù)。由于電流信號難以采集，所以首先通過I/V轉(zhuǎn)換電路將電流信號轉(zhuǎn)換為電壓信號，如圖2所示。

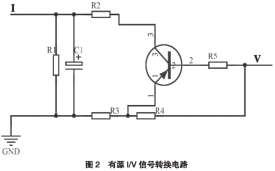
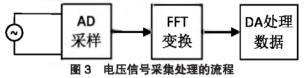
電流信號轉(zhuǎn)換為電壓信號之后，信號的采集、分析和處理過程如圖3所示。

假設(shè)采集到的電機(jī)工作時的信號為一周期性信號，即輸入的信號中除基波外，只包含恒定的直流分量和各種整次諧波分量。此時電流輸入信號可以表示為:

其中，a₀、a_k、b_k為傅里葉系數(shù)

由數(shù)學(xué)定理可知周期函數(shù)可展開為傅里葉級數(shù):

其中，式(7)和式(11)的各系數(shù)之間還有以下關(guān)系:

當(dāng)采集到電壓信號后，A_km和φ_k分別對應(yīng)電壓的k次諧波的幅值A_kmk次諧波的相位φ，由此可以計(jì)算出電壓的k次諧波的有效值。得出系數(shù)之間的關(guān)系后還可以得到k次諧波的有功功率P_k、無功功率Q_k和視在功率S_k.

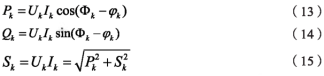
同時可以計(jì)算出k次諧波的電壓含有率HRU_k ：

同理得到電壓的諧波總失真度THD_U：

3基2時間抽取FFT算法的分析

設(shè)序列x[k]的長度為用N=2^M為正整數(shù)，M為正整數(shù)，長度不滿足該條件，可通過補(bǔ)0的方法使序列x[k]滿足該條件。對長度為N的序列x[k]進(jìn)行時間抽取，將其分解為兩個

長度為N/2點(diǎn)的序列 ，分別為 ：

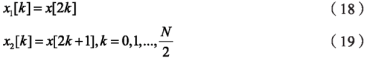
其中，x₁[k]是序列中偶數(shù)點(diǎn)構(gòu)成的序列，x₂[k]是序列中奇數(shù)點(diǎn)構(gòu)成的序列。

對x[k]進(jìn)行DFT得：

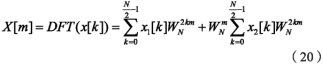
由于旋轉(zhuǎn)因子W_Nⁿ擁有式(4)、式(5)和式(6)的特性,因此：

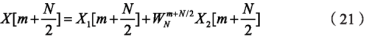
綜上所述，可以表示為：

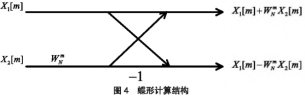
將式(22)和式(23)合并即可得到序列x[k]的DFT。蝶形計(jì)算結(jié)構(gòu)如圖4所示。

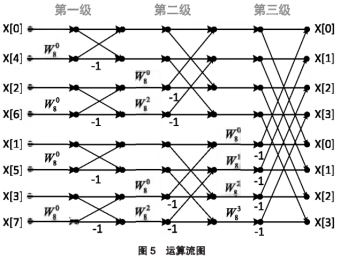
基2時間抽取FFT運(yùn)算流圖(N=8)如圖5所示。

4仿真結(jié)果

實(shí)際中常常會遇到要求兩個序列的線性卷積，如一個信號序列x(n)通過FIR濾波器時，其輸出y(n)應(yīng)是x(h)與h(n)的卷積：

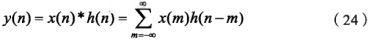
有限長序列x(n)與h(n)的卷積結(jié)果y(n)也是一個有限長序列。假設(shè)x(n)和h(n)的長度分別為N1和N2,則y(n)的長度為N1+N2-1。若通過補(bǔ)0使x(n)和h(n)都加長到N點(diǎn),就可以用圓周卷積計(jì)算線性卷積。這樣得到用FFT運(yùn)算來求y(n)值(快速卷積)的步驟如下。

(1) 對序列x(n)和h(n)補(bǔ)0至長為N,使得N≥N1+N2-1,,并且N=2^M(M為整數(shù))，即：

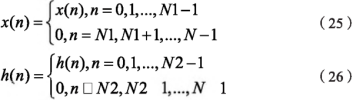
(2)用FFT計(jì)算x(n)與h(n)的離散傅里葉變換:

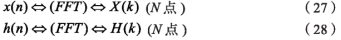
(3)計(jì)算XQ=X(QH(Q。

(4)用IFFT計(jì)算Y(k)的離散傅里葉反變換得：

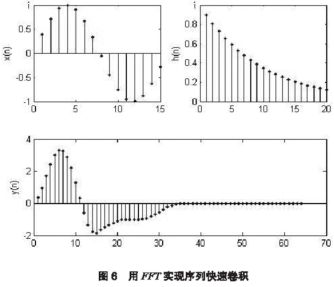
例如，運(yùn)用FFT實(shí)現(xiàn)序列x(n)=sin(0.4n),1≤n≤15與序列y(n)=0.9ⁿ,1≤n≤20之間的快速卷積，并測試直接卷積與快速卷積的時間，得到的卷積結(jié)果如圖6所示。其中，運(yùn)用快速卷積的時間為0.000033秒，運(yùn)用直接卷積的時間為0.000049秒。很明顯，運(yùn)用FFT的快速卷積運(yùn)算速度上優(yōu)于宜接卷積。

5.安科瑞智能電動機(jī)保護(hù)器介紹

5.1產(chǎn)品介紹

智能電動機(jī)保護(hù)器(以下簡稱保護(hù)器)，采用單片機(jī)技術(shù)，具有抗干擾能力強(qiáng)、工作穩(wěn)定可靠、數(shù)字化、智能化、網(wǎng)絡(luò)化等特點(diǎn)。保護(hù)器能對電動機(jī)運(yùn)行過程中出現(xiàn)的過載、斷相、不平衡、欠載、接地/漏電、堵轉(zhuǎn)、阻塞、外部故障等多種情況進(jìn)行保護(hù)，并設(shè)有SOE故障事件記錄功能，方便現(xiàn)場維護(hù)人員查找故障原因。適用于煤礦、石化、冶煉、電力、以及民用建筑等領(lǐng)域。本保護(hù)器具有RS485遠(yuǎn)程通訊接口，DC4-20mA模擬量輸出，方便與PLC、PC等控制機(jī)組成網(wǎng)絡(luò)系統(tǒng)。實(shí)現(xiàn)電動機(jī)運(yùn)行的遠(yuǎn)程監(jiān)控。

5.2技術(shù)參數(shù)

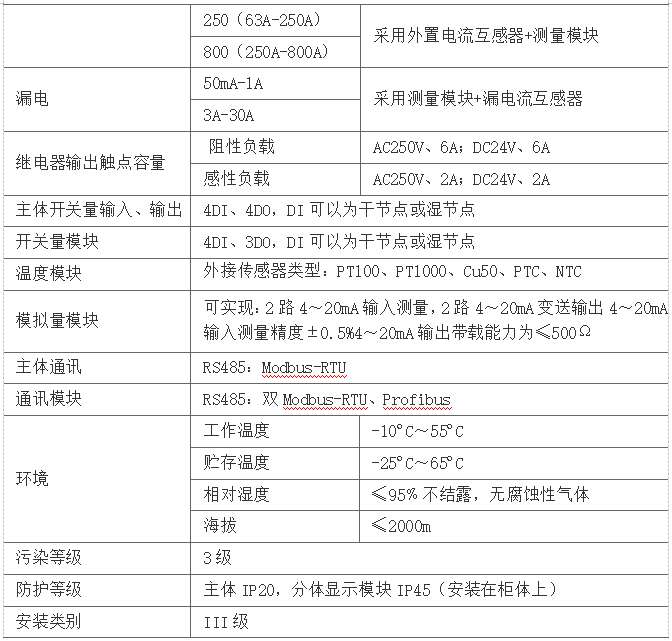
5.2.1數(shù)字式電動機(jī)保護(hù)器

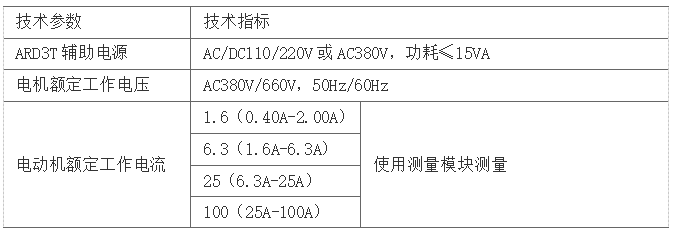
5.2.2模塊式電動機(jī)保護(hù)器

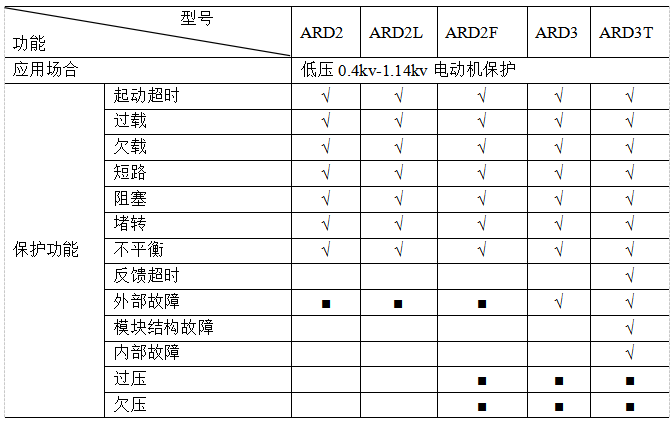
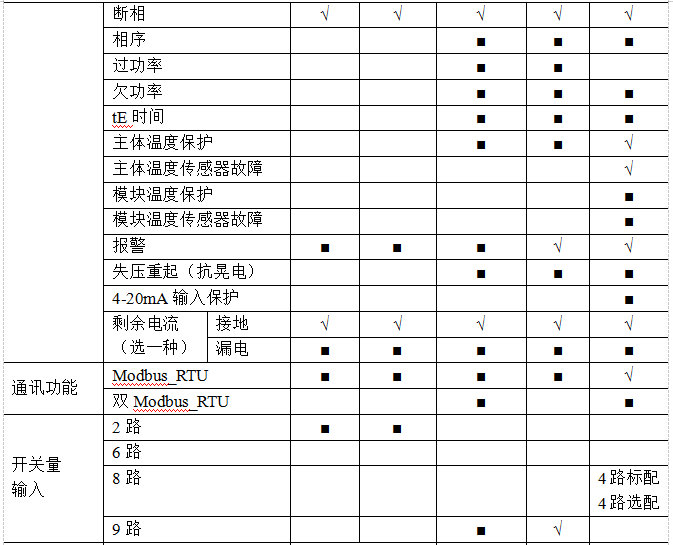
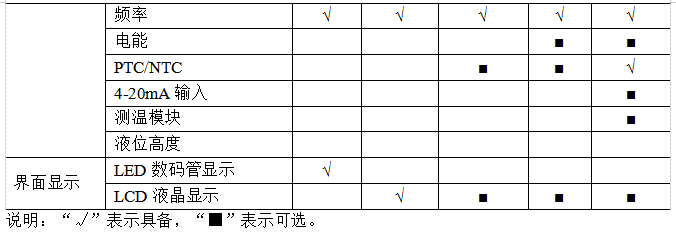
5.3產(chǎn)品選型

6 結(jié)束語

本文研究了一種由DFT優(yōu)化演變而來的FFT算法，與傳統(tǒng)方法相比，該算法具有高效的運(yùn)算效率，為信號處理提供了良好的條件。仿真結(jié)果證明，該算法能夠減少信號處理所需的時間，可以直接計(jì)算出電壓信號的直流分量以及各次諧波的幅值和相位，便于分析諧波的分量，有利于繼電器及時做出斷電的決策。

參考文獻(xiàn)

[1] 李加升，熊潔，陽磊.基于FFT算法的電流信號檢測裝置設(shè)計(jì)[J].湖南城市學(xué)院學(xué)報(自然科學(xué)版),2020,29(6):58-62.

[2] 李哲，李明.電力電子裝置高精度FFT方法對比分析[J].科學(xué)技術(shù)新,2020(30):43-44.

[3] 姜翟躍，徐浩南，巫樂文，張敬昊，江豪杰.FFT算法在電機(jī)保護(hù)系統(tǒng)中的應(yīng)用分析

[4] 安科瑞企業(yè)微電網(wǎng)設(shè)計(jì)與應(yīng)用手冊.2020.06版

作者簡介：侯文莉，女，安科瑞電氣股份有限公司，主要研究方向?yàn)橹悄茈娋W(wǎng)供配電